论文信息
| Title | Authors |
|---|---|
| Using Statistical Image Model for JPEG Steganography: Uniform Embedding Revisited | Linjie Guo, Jiangqun Ni, Wenkang Su, Chengpei Tang, and Yun Qing Shi |
概述
UERD这篇论文主要工作可以概况为以下三点:
- 使用了所有的DCT系数(包括DC和零AC系数在内)作为载体元素
- 基于DCT块和每个DCT系数的模式来构造失真函数
- 计算复杂度可忽略不计,更实用
对UED的攻讦
UED存在的问题主要有两点:
-
对原始的均匀嵌入(UE)策略可以从信息论的视角来理解,即离散源的最大熵原理。但是对于自然图像来说,不同大小的DCT系数可容忍的相对变化是不同的。就是说,对两种值不同的系数进行相同的修改,造成的影响是不同的。
-
对修改的“均匀扩展”是否真的能够得到最佳的安全性?
广义均匀嵌入策略(Generalized Uniform Embedding)
UED的核心思想是将嵌入造成的修改均匀扩散到全体DCT系数中,而UERD的核心思想是将“检测能力”均匀扩散到全体系数。
上一篇文章介绍UED时提到了变异系数这个概念。变异系数Cv在一阶二阶统计上都表现出了随系数增大而增大的特性,换句话说,就是对系数的检测能力随着系数增大会下降。
UE中采用的是$1/|x|$这种衡量失真的形式,目的在于使得每种系数被选择到用来修改的**“概率”**一样,以达到均匀嵌入的目的。但实际上,这只是不同大小的系数被选择嵌入的概率是均匀的,而非真正意义上的均匀嵌入。因为不同大小的系数进行同样的修改,检测到的影响是不同的。越大的系数进行修改造成的影响越小。
因此,更合理的选择策略实要将这种“检测能力”均匀扩散到整个系数空间中。为此,需要控制每种系数的相对变化与变异系数$Cv$成比例就可。这种思想叫做广义均匀嵌入策略(Generalized Uniform Embedding)。
UERD(Uniform Embedding Revisted Distortion)设计
实现广义均匀嵌入的一般做法是增加具有更大的CV的系数的嵌入几率。
因为单单比较系数并不能表示任何统计特性,因此作者研究了系数的位置对于CV的影响。而位置的影响主要包括的是AC模式和DCT块来表示。
注:这里对AC模式没有进行解释,从上下文内容来看,我猜测是说AC系数在块中的位置,因为文中提到说模式00指的是DC模式,而DC的位置就是左上角也就是位于(0,0)处。下文中所有提到的AC模式,都默认按照AC系数在DCT块中的位置来理解,如AC模式10就是指位于(1,0)位置上的AC系数值得统计直方图。
首先,作者探究了不同AC模式的统计特性,统计结果表明,AC模式所处频率越高(右下角),对应的AC系数中拥有的零系数越多,对应的CV值也越低。说明这些系数被选择修改的概率越低。
然后,作者探究了具有不同纹理复杂度的块的统计特性。这里衡量纹理复杂度的方式是根据块中非零系数的个数来评判。非零系数越少,复杂度越低。文中将复杂度分级为如下四类:

拿第一类来说明,块中非零AC系数个数在0-8之间时,就被分类为最低的纹理复杂度水平。
统计结果表明,DCT块中零AC系数个数越多,也就是纹理复杂度越低,对应的CV值就越低,这些块被选择来修改的概率越低。

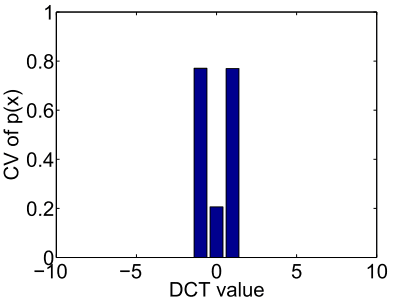
从图2可以看出,零AC系数的CV值在相同模式下也存在比其他非零AC系数值高的情况。而用图2和图3对比可以看出,低频AC模式下的零系数CV值是高于高频AC模式下的零系数CV值的。
结合这两种实验数据可以看出,低频AC模式下的零系数CV值高于高频AC模式下的零系数CV值,甚至高于相同模式下的非零系数CV值。而高纹理复杂度下得零系数CV值比低纹理复杂度下的要高很多,甚至比低纹理复杂度下的其他非零系数CV值都要高。
这两种情况都证明了确实存在有比一些非零AC系数更适合嵌入的零AC系数。
基于以上发现,作者定义了均匀嵌入重访失真(Uniform Embedding Revisted Distortion)函数$\rho_{ij}$。
用$x_{ij}$表示在$(i,j)$位置上的DCT系数,$\rho_{ij}$定义如下:
$$\rho_{ij}=\rho_{ij,mode}\cdot \rho_{ij,block}$$
其中$\rho_{ij,mode}$和$\rho_{ij,block}$分别对应于AC模式和DCT块的失真度量。这两个度量的选择有很多种。作者在论文里将AC模式的失真度量定义为对应位置上的量化步长。而DCT块的失真度量定义为$x_{ij}$所属块以及相邻块的能量函数。 假设$x_{ij}$处在第$mn$块中,那么它的块能量$D_{mn}$定义如下:
$$D_{mn}=\sum^7_{k=0}\sum^7_{l=0}|x_{kl}|\cdot q_{kl}$$
其中$x_{kl}$表示的是块中对应位置上的系数值,并且设$x_{00}=0$来避免DC系数造成的影响,$q_{kl}$就是对应位置上的量化步长。
最终$\rho_{ij}$就可以表示如下:

(公式有点复杂,不想写latex公式了,偷个懒,哈哈)
其中$\hat{D}={D_{(m-1)(n-1)},D_{(m-1)n},D_{(m-1)(n+1)},D_{m(n-1)},D_{m(n+1)},D_{(m+1)(n-1)},D_{(m+1)n},D_{(m+1)(n+1)}}$
是第$mn$个块的相邻八个块的块能量。
考虑到DC系数的统计特性与AC系数有很大不同,这里作者启发式地将DC系数的失真定义为相邻的AC系数的均值。
结语
UERD的介绍到此为止,最近调研文献时又发现了一篇18年的TCSVT,文章是对UERD进行的进一步改进,还是他们课题组的。具体没有细看,等有机会阅读完之后再决定是否介绍那一篇吧。